find tangent lines through a point (a,b) out of a circle x^2+y^2=r^2.
tangent lines : y = m(x-a)+b ⇔ mx - y - am + b = 0, where m represents the gradient of the the tangent lines.
the distance between the point (0,0) which is the center of the circle and the tangent lines is
|-am+b|
--------------
root(m^2+1)
= r
⇔ (a^2-r^2)m^2-2abm+b^2-r^2=0
⇔ m =
ab ± root(r^2(a^2+b^2-r^2))
-------------------------------------
a^2-r^2
therefore, the tangent lines are
y =
ab ± root(r^2(a^2+b^2-r^2))
------------------------------------- (x-a) + b
a^2-r^2
<question>
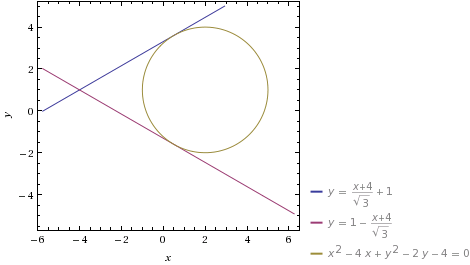
find the tangent lines through a point (-4,1) out of a circle x^2+y^2-4x-2y-4=0.
<answer>
x^2+y^2-4x-2y-4=0 ⇔ (x-2)^2+(y-1)^2=9
moving the center of the circle (2,1) to (0,0),
the point (-4,1) to(-6,0).
therefore
m =
0 ± root(9(36+0-9))
-------------------------------
36-9
= ±1/root(3)
therefore, by m=±1/root(3) and (-4,1) ,
y = ±1/root(3)(x + 4) + 1

Write a comment