For x, y in C,
Consider simultaneous equations of x and y
x + y = u
xy = v.
Let the solutions be x = α and y = β.
Thus
α+β = u
αβ = v.
A quadratic equation whose solutions are α and β is
t² -ut+v =0.
By α, β in C, u and v are also in C.
Here, considering α, β in R, the solutions of t² -ut+v =0 must be real solutions.
Hence u²-4v≧0 holds.
Image
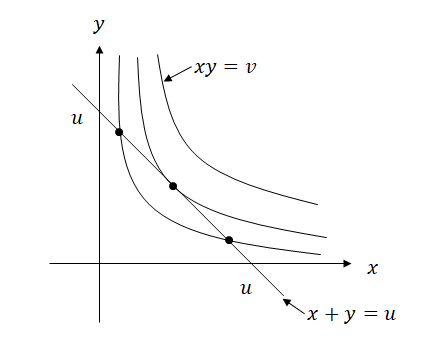
By
x + y = u
xy = v, we have
x²-ux+v=0.
By x in R,
u² - 4v ≧ 0
